Remarque préliminaire : cet exercice ne peut être effectué qu’après l’exercice Application répartie entre threads – Partie I.

La solution de l’exercice ci-dessus présente deux inconvénients majeurs liés :

1. l’arborescence des appels de CNp() présente de très nombreux noeuds identiques, comme le montre l’exemple C(5,3) ci-dessous :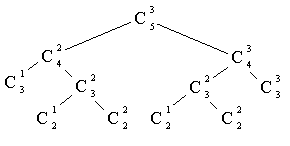

   
   
   
   Figure 1

2. puisque chaque noeud correspond à la création d’un thread, et puisque leur nombre est limité, il est probable que le nombre maximal soit très vite atteint.

L’exercice proposé ici consiste à ne lancer un thread que si la combinaison correspondante n’a pas été déja calculée, ou si elle n’est pas en cours de calcul.

Cette technique est connue en informatique sous le nom de .

Pour cela, on utilise une matrice à deux dimensions, Combin qui mémorise les valeurs de C(i, j) avec 1 <= i <= N, et 1 <= j <= p.

Celle-ci est supposée déclarée au début de l’espace de noms, à des dimensions suffisantes.

Conventionnellement, on utilisera les valeurs suivantes :

Combin [i][j] = -1        : C(i, j) non calculée
Combin [i][j] =  0        : C(i, j) en cours de calcul
Combin [i][j] =  x > 0    : C(i, j) déjà calculée

Pour simplifier le traitement, Combin[i][j] correspond à C(i, j).

Pour cela, une ligne correspondant à i = 0 et une colonne correspondant à j = 0 ont été ajoutées au tableau.

Avant le début du calcul, la matrice Combin doit être initialisée.

Pour N = 5 et p = 3 par exemple, elle prend les valeurs suivantes :

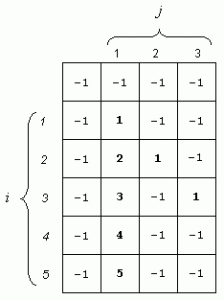
Vous remarquez que certaines valeurs initiales découlent immédiatement de la définition et n’ont pas besoin d’être calculées pour être connues : les C(i, i) et C(N, 1).

Elles ont donc été directement placées dans la matrice.

La figure suivante représente le contenu de la matrice Combin après la fin du calcul de C(5, 3).

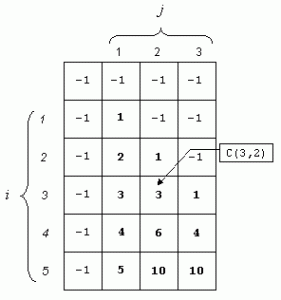
Travail à effectuer

Créer le projet CNpThreadsBoostV2.

Télécharger le fichier

Navigation des articles