Il existe une fonction de recherche générique standard très
puissante :
template <class InputIterator, class Predicate>
InputIterator find_if (InputIterator first, InputIterator last,
Predicate pred);
Comme son nom l’indique, elle recherche, entre les itérateurs first et last d’un conteneur, la position du premier élément qui satisfait une condition, représentée par le functor pred qui doit être un prédicat.
Cela signifie que la surcharge de l’opérateur () a le
profil suivant :
bool operator () const (const T &);
Le principe en est le même que précédemment.
Travail à effectuer
Créer le projet FunctorFind.
Copier dans le fichier main.cpp le fichier de test FunctorSort.cpp FunctorSort.cpp, qui est le corrigé de l’exercice FunctorSort Functors et algorithmes de tri” ci-dessus.
/**
*
* @file FunctorSort.cpp
*
* @authors M. Laporte, D. Mathieu
*
* @date 07/12/2011
*
* @version V1.0
*
**/
#include <string>
#include <vector>
#include <algorithm> // sort()
#include <iostream>
using namespace std;
namespace
{
template <typename T>
class ILessThanGen
{
public :
virtual ~ILessThanGen (void) {}
virtual bool operator () (const T &, const T &) const = 0;
}; // ILessThanGen
class Pers
{
string myNom;
unsigned myAge;
public :
Pers (const string & Nom, unsigned Age)
: myNom (Nom), myAge (Age) {}
const string & getNom (void) const noexcept { return myNom; }
unsigned getAge (void) const noexcept { return myAge; }
private :
ostream & display (ostream & os) const
{
return os << getAge () << " - " << getNom ();
} // display()
public :
friend ostream & operator << (ostream & os, const Pers & p)
{
return p.display (os);
}
}; // Pers
class TriParAgeAsc : public ILessThanGen <Pers>
{
public :
virtual ~TriParAgeAsc (void) noexcept {}
virtual bool operator () (const Pers & p1, const Pers & p2)
const noexcept
{
return p1.getAge () < p2.getAge ();
} // operator ()
}; // TriParAgeAsc
class TriParNomDesc : public ILessThanGen <Pers>
{
public :
virtual ~TriParNomDesc (void) noexcept {}
virtual bool operator () (const Pers & p1, const Pers & p2)
const noexcept
{
return p1.getNom () > p2.getNom ();
} // operator ()
}; // TriParNomDesc
void functorSort (void)
{
cout << "FunctorSort : \n";
typedef vector <Pers> CVPers;
CVPers vPers;
vPers.push_back ( Pers ("Charlotte", 21));
vPers.push_back ( Pers ("Alfred", 12));
vPers.push_back ( Pers ("Jean", 42));
vPers.push_back ( Pers ("Noemie", 11));
vPers.push_back ( Pers ("Berthe", 99));
vPers.push_back ( Pers ("Agathe", 29));
vPers.push_back ( Pers ("Sylvain", 42));
vPers.push_back ( Pers ("Pierre", 75));
cout << "\nTri par age croissant\n\n";
sort (vPers.begin (), vPers.end (), TriParAgeAsc ());
for (const Pers & personne : vPers)
cout << personne << '\n';
cout << "\nTri par nom decroissant\n\n";
sort (vPers.begin (), vPers.end (), TriParNomDesc ());
for (const Pers & personne : vPers)
cout << personne << '\n';
} // functorSort()
} // namespace
int main (void)
{
functorSort ();
return 0;
} // main()
Remplacez la classe ILessThanGen par IPredicatGen et supprimez tout ce qui concerne les tris.
Dérivez publiquement cette classe en SelParTrancheAge, qui possède :
myAgeMin et myAgeMax,(), qui renvoie true lorsque l’âge de l’élément qui lui est passé en paramètre est dans l’intervalle [myAgeMin, myAgeMax].Testez en utilisant et en complétant la fonction suivante :
void functorFind (void)
{
cout << "FunctorFind : \n";
typedef vector <Pers> CVPers;
CVPers vPers;
vPers.push_back ( Pers ("Charlotte", 21));
vPers.push_back ( Pers ("Alfred", 12));
vPers.push_back ( Pers ("Jean", 42));
vPers.push_back ( Pers ("Noemie", 11));
vPers.push_back ( Pers ("Berthe", 99));
vPers.push_back ( Pers ("Agathe", 29));
vPers.push_back ( Pers ("Sylvain", 42));
vPers.push_back ( Pers ("Pierre", 75));
for (const Pers & personne : vPers)
cout << personne << '\n';
CVPers::const_iterator pos;
cout << "\nRecherche sur 43 <= age <= 75 : ";
pos = find_if (vPers.begin (), vPers.end (), // a completer
if (vPers.end () ==pos)
cout << "Aucun element ne correspond a ce critere\n";
else
cout << *pos << '\n';
cout << "\nRecherche sur 43 <= age <= 45 : ";
pos = find_if (vPers.begin (), vPers.end (), // a completer
if (vPers.end () == pos)
cout << "Aucun element ne correspond a ce critere\n";
else
cout << *pos << '\n';
cout << '\n';
} // functorFind()
Lorsque vous obtenez des résultats conformes à l’affichage attendu ci-dessous,
FunctorFind : 21 - Charlotte 12 - Alfred 42 - Jean 11 - Noemie 99 - Berthe 29 - Agathe 42 - Sylvain 75 - Pierre Recherche sur 43 <= age <= 75 : 75 - Pierre Recherche sur 43 <= age <= 45 : Aucun element ne correspond a ce critere
IPredicatGen en SelParNomMin, qui possède :
myNomMin,(), qui renvoie true lorsque le nom de l’élément qui lui est passémyNomMin.functorFind() la séquence suivante :
cout << "\nRecherche sur nom > Noemie : ";
pos = find_if (vPers.begin (), vPers.end (), // a completer
if (vPers.end () == pos)
cout << "Aucun element ne correspond a ce critere\n";
else
cout << *pos << '\n';
cout << "\nRecherche sur nom > alfred : ";
pos = find_if (vPers.begin (), vPers.end (), // a completer
if (vPers.end () == pos)
cout << "Aucun element ne correspond a ce critere\n";
else
cout << *pos << '\n';
Vous devez obtenir des résultats conformes à la deuxième partie de l’affichage attendu ci-dessous.
Lorsque les affichages sont corrects, une dernière modification est proposée : on remarque que la classe IPredicatGen manque encore de généralité, car le résultat est toujours un booléen (c’est pour cela que c’est un prédicat).
En réalité, dans certaines applications, on peut supposer avoir besoin de functors à un seul paramètre qui renvoient des types différents du type booléen.
Il suffit d’ajouter en second paramètre de généricité le type de retour : cela s’appelle une fonction-objet unaire ou unary function.
Ajoutez la classe IUnaryFunction, copie de IPredicatGen, à laquelle est ajouté le second paramètre de généricité TRes représentant le type de retour de la fonction.
Modifiez les deux classes SelParTrancheAge et SelParNomMin, en en faisant des UnaryFunction‘s et tester à nouveau.
résultats supplémentaires attendus :
Recherche sur nom > Noemie : 42 - Sylvain Recherche sur nom > alfred : Aucun element ne correspond a ce critere
Remarque préliminaire : cet exercice ne peut être effectué qu’après l’exercice précédent.
L’exercice nécessite l’utilisation de la fonction rand() qui a déjà été mise à votre disposition.
Lorsque vous en avez fini, récupérer les fichiers sources du projet DureeRelOps dans le nouveau projet DureeSortSearch.
Dans la fonction TestDuree() :
KDureeMax représentant la valeur maximale d’une durée (par exemple 1000000),CVDuree (vecteur de Durees) et Iter_t (itérateur de lecture (const_iterator)) et un vecteur de type CVDuree :[0, KDureeMax],[ xx:xx:xx:xx] = yyyyyyy
où yyyyyy est la valeur de la durée en secondes,
sort() (#include <algorithm>),L’objectif de cet exercice est de construire une ébauche d’une classe permettant de gérer une durée de temps (un délai), exprimé soit en secondes, soit en jours, heures, minutes et secondes.
Les normes IUT de programmation C++ devront être respectées : identificateurs des données membres (myData), identificateurs des paramètres (Data, terminaisons des classes}; // CX, …).
Création du projet
Créez le projet DureeDeBase (avec QT Creator).
Etape 1
Dans l’espace de noms anonyme du fichier main.cpp, déclarer la classe Duree dont le diagramme de classe est
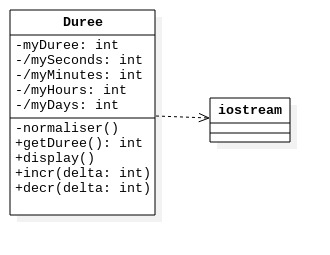
, qui possède les données membres suivantes :
la durée en secondes (toujours positive ou nulle, et la plus grande possible),
le nombre de jours, d’heures, de minutes et de secondes correspondants (choisir les types les mieux adaptés).
et les fonctions membres suivantes :
un constructeur dont l’unique paramètre est le nombre de secondes de la durée,
une fonction membre display()
0 jour(s) 0 heure(s) 1 minute(s) 40 seconde(s)
12 jour(s) 23 heure(s) 59 minute(s) 9 seconde(s)
Comme le montre l’exemple ci-dessus, prévoir pour les zones numériques un format tel qu’elles soient alignées verticalement (rappel en utilisant le manipulateur standard setw().
On pourra simplifier l’affichage en utilisant les unités h., j. min., s. au lieu de jour, heure, minute, seconde.
une fonction membre normaliser()
Cette fonction ne devrait être accessible qu’à des fins internes.
Les définitions (corps) de toutes les fonctions membres devront être faites en dehors de la déclaration de la classe.
Attention à utiliser à bon escient le qualificatif const.
Avant de continuer à développer cette classe, tester ces trois premières fonctions membres.
Pour cela, écrire la fonction testDureeDeBase()Duree initialisé à la valeur lue et l’affiche à l’écran.
Compiler et tester.
Lorsque les résultats vous sembleront justes, vous devez ouvrir un terminal et vous placer dans le répertoire où se trouve l’exécutable de votre projet.
Téléchargez-y le fichier FichDurees.
Testez à nouveau votre programme en redirigeant le fichier FichDurees sur le flux d’entrée standard et comparez vos résultats avec ceux qui sont indiqués ci-dessous.
Seconde étape
Vous pouvez maintenant enrichir la classe avec :
la fonction membre getDuree()
les fonctions membres incr()decr()delta passée en paramètre.
On considère pour le moment que si delta est supérieur à la valeur courante de la durée, le résultat de decr(Delta)
En fin de fonction testDureeDeBase()
Duree d1 (0);
d1.incr (1);
cout << "Nbre sec. " << setw (6) << d1.getDuree ()
<< ", soit : ";
d1.display ();
cout << '\n';
d1.decr (1);
cout << "Nbre sec. " << setw (6) << d1.getDuree ()
<< ", soit : ";
d1.display ();
cout << '\n';
d1.incr (3662);
cout << "Nbre sec. " << setw (6) << d1.getDuree ()
<< ", soit : ";
d1.display ();
cout << '\n';
d1.decr (10000);
cout << "Nbre sec. " << setw (6) << d1.getDuree ()
<< ", soit : ";
d1.display ();
cout << '\n';
N’oubliez pas de sauvegarder tous vos fichiers sources sur github.
L’intérêt du parallélisme est double :
profiter de la puissance de traitement des machines multi-processeurs,
confier à chaque thread une activité spécifique beaucoup plus facile à concevoir et maintenir qu’au sein d’un gros programme.
Rappel : le nombre de combinaisons de N objets (N > 0) pris p à p (p <= N), noté C (N, p)
C (N, p) = N si p = 1 C (N, p) = 1 si p = N C (N, p) = C (N-1, p-1) + C (N-1, p) dans les autres cas
Il peut être calculé récursivement par :
unsigned CNp (unsigned N, unsigned p)
{
return (N == p) ? 1 : (p == 1) ? N : CNp (N-1, p-1) + CNp (N-1, p);
} // CNp()
// programme appelant :
...
Result = CNp (NbTot, Nb);
...
Il vous est demandé de remplacer chaque appel de la fonction récursive CNp() par la création d’un thread qui calcule la valeur correspondante.
A son tour, chaque thread lance 2 threads dont il attend le résultat (ou aucun) avant de se terminer lui-même.
Le main_thread lance un thread avec les valeurs initiales N et p et attend sa fin.
Travail à effectuer
Créer le projet CNpThreadsBoostV1.
Dans l’espace de noms anonyme du fichier CNpThreadsBoostV1.cpp, écrire la fonction thread CNp() qui effectue le calcul C(N, p), selon cette méthode.
N et p lui sont passés en paramètre(s).
En principe, elle devrait renvoyer le résultat, mais une fonction-thread ne renvoie pas de résultat (void).
Il ne reste plus qu’à en faire une procédure (utiliser un paramètre-résultat supplémentaire !).
Attention et rappel : les paramètres d’une fonction-thread sont toujours passés par valeur …
Pour créer un thread on utilisera la fonction bind(), de la bibliothèque functional,
qui renvoie un callable, qui lie son premier paramètre (une fonction), avec tous les autres paramètres de
bind() qui sont, dans l’ordre, les paramètres de la fonction premier paramètre de bind.
Exemple :
void f (int P1, char P2, int * P3); int Val; bind (f, 12, 'c', & Val) // est un callable
Ecrire la fonction main() qui amorce le calcul réparti, en utilisant les valeurs N et p passées en arguments de la commande (à vérifier), et qui affiche le résultat.
Remarque préliminaire : cet exercice ne peut être effectué qu’après l’exercice Application répartie entre threads – Partie I.
La solution de l’exercice ci-dessus présente deux inconvénients majeurs liés :
l’arborescence des appels de CNp() présente de très nombreux noeuds identiques, comme le montre l’exemple C(5,3) ci-dessous :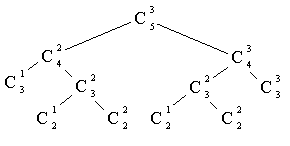
Figure 1
puisque chaque noeud correspond à la création d’un thread, et puisque leur nombre est limité, il est probable que le nombre maximal soit très vite atteint.
L’exercice proposé ici consiste à ne lancer un thread que si la combinaison correspondante n’a pas été déja calculée, ou si elle n’est pas en cours de calcul.
Cette technique est connue en informatique sous le nom de .
Pour cela, on utilise une matrice à deux dimensions, Combin qui mémorise les valeurs de C(i, j) avec 1 <= i <= N, et 1 <= j <= p.
Celle-ci est supposée déclarée au début de l’espace de noms, à des dimensions suffisantes.
Conventionnellement, on utilisera les valeurs suivantes :
Combin [i][j] = -1 : C(i, j) non calculée Combin [i][j] = 0 : C(i, j) en cours de calcul Combin [i][j] = x > 0 : C(i, j) déjà calculée
Pour simplifier le traitement, Combin[i][j] correspond à C(i, j).
Pour cela, une ligne correspondant à i = 0 et une colonne correspondant à j = 0 ont été ajoutées au tableau.
Avant le début du calcul, la matrice Combin doit être initialisée.
Pour N = 5 et p = 3 par exemple, elle prend les valeurs suivantes :
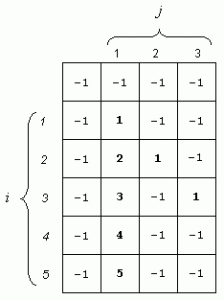
Vous remarquez que certaines valeurs initiales découlent immédiatement de la définition et n’ont pas besoin d’être calculées pour être connues : les C(i, i) et C(N, 1).
Elles ont donc été directement placées dans la matrice.
La figure suivante représente le contenu de la matrice Combin après la fin du calcul de C(5, 3).
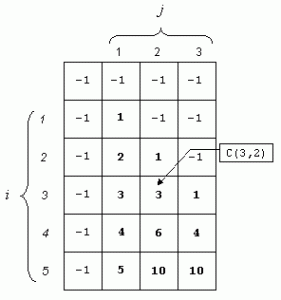
Travail à effectuer
Créer le projet CNpThreadsBoostV2.
Télécharger le fichier
Compléter le code suivant : Ecrire les fonctions duales de celles de l‘exercice 16 de façon a transformer une ligne / l’intégralité du vecteur encodé en transformant chaque (chaine de) caractères de l’alphabet Leet en alphabet “standard“. Modifier le M4104C Amphi
M4104C
#include <iostream>
#include <vector>
#include <iomanip>
#include <cstdlib>
#include <ctime>
#include <algorithm>
#include <thread>
using namespace std;
typedef vector <unsigned> CVUint;
typedef vector < vector <double>> CMatrix;
CMatrix Mat;
void SelectSort (CVUint & VUint)
{
for (unsigned i (0); i < VUint.size(); ++i)
{
CVUint::iterator Min (min_element (VUint.begin() + i, VUint.end()));
swap (VUint[i],VUint [Min - VUint.begin()]);
}
}
void InsertSort (CVUint & VUint)
{
for (unsigned i (1); i < VUint.size(); ++i)
{
unsigned Val (VUint [i]);
unsigned j (i);
for (; j > 0 && VUint[j - 1] > Val; --j)
VUint[j] = VUint[j - 1];
VUint[j] = Val;
}
}
void BubbleSort (CVUint & VUint)
{
for (unsigned i (VUint.size()); i -- > 0; )
{
bool TableauTrie = true;
for (unsigned j (0); j < i ; ++j)
{
if (VUint[j + 1] < VUint[j])
{
swap (VUint[j + 1], VUint[j]);
TableauTrie = false;
}
}
if (TableauTrie) return;
}
}
void LanguageSort (CVUint & VUint)
{
sort (VUint.begin(), VUint.end());
}
void InitMat (unsigned NbColumns)
{
Mat.resize(4, vector <double> (NbColumns));
}
void protoGenericSort(void (*Sort) (CVUint & VUint), const CVUint & VUint, unsigned NbFois, unsigned PosMat, unsigned VectNum)
{
for (unsigned i (0); i < NbFois; ++i)
{
CVUint CopyVUint (VUint);
/* TODO*/
double elapsed;
/* TODO*/
Sort (CopyVUint);
/* TODO*/
Mat [PosMat][i + NbFois * VectNum] = elapsed;
}
}
void TraiterResultats (unsigned NbElemAEnlever)
{
for (vector <double> & UneLigne : Mat)
{
//tri
sort (UneLigne.begin(), UneLigne.end());
//plus petit temps
double min (UneLigne[0]);
//plus grand temps
double max (UneLigne[UneLigne.size()-1]);
//temps median
double med (UneLigne[UneLigne.size()/2]);
//On assigne les valeurs memorisees aux 3 premières cases
UneLigne[0] = min;
UneLigne[1] = med;
UneLigne [2] = max;
}
//Affichage
cout << setw (20) << "Tri" << setw (10) << "Min" << setw (10) << "Med" << setw (10) << "Max" << endl;
vector<string> VMetode {"Selection", "Insertion", "Bulles", "Langage"};
for (unsigned i (0); i < VMetode.size(); ++i)
cout << setw (20) << VMetode[i] << setw (10) << setprecision(6) << Mat[i][0] << setw (10) << setprecision(6) << Mat[i][1] << setw (10) << setprecision(6) << Mat[i][2] << endl;
}
int main(int argc, char *argv[])
{
if (argc != 4)
{
cerr << "boulette !\n utilisation : " << argv [0] << " (1) NbElem par vecteur (2) Nb de vecteurs differents (3) Nb itérations par vecteur" << endl;
return 1;
}
unsigned NbElem (stoul(argv[1]));
unsigned NbVecteurs (stoul(argv[2]));
unsigned NbFois (stoul(argv[3]));
srand (time(NULL));
CVUint VUInt (NbElem);
InitMat(NbFois * NbVecteurs);
for (unsigned i (0); i < NbVecteurs; ++i)
{
for (auto & Val : VUInt)
Val = rand () % (VUInt.size() * 10);
thread th1 (/* TODO*/);
thread th2 (/* TODO*/);
thread th3 (/* TODO*/);
thread th4 (/* TODO*/);
th1.join();
th2.join();
th3.join();
th4.join();
cout << i << "fini" << endl;
}
cout << "Taille des vecteurs : " << NbElem << "\nNb de vecteurs : " << NbVecteurs << "\nNb iterations par vecteur : " << NbFois << endl;
TraiterResultats (NbFois * NbVecteurs / 10);
return 0;
}
M1103 – Amphi2
M1102 – TP6 – Exercice 17
main () pour prendre en compte ses deux fonctions. L’appel de ces fonctions se fait en saisissant la chaine « unl» suivie de « tout » ou d’un numéro de ligne.